Quantitative Finance

Modern Portfolio Theory has become pervasive due to its effectiveness, simplicity and formal foundation. However, with time, its assumptions have become less valid and its primary purpose, risk reduction, has become more difficult to acheive. Our goal here is to determine if one can make a slight change to the theory and still acheive:

Asset growth over the long term.
Risk reduction, with as few negative results over time as possible.
A tractable formalism with the same intellectual rigor as Modern Portfolio Theory, while still permitting easy calculation.

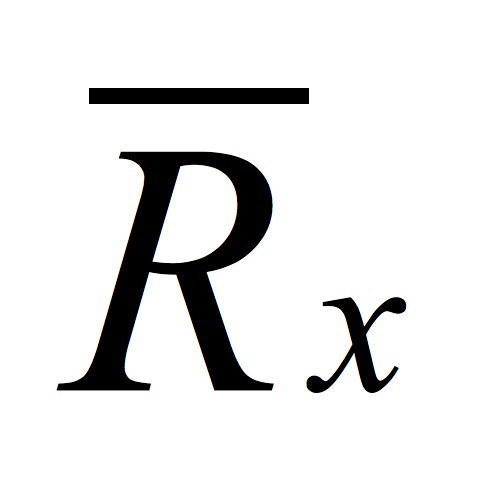Hellmut D Scholtz's paper takes a step in this direction by slightly changing Modern Portfolio Theory to better model "up" and "down" markets. He starts with the Single-index model (German) of Asset Pricing:

where:

is the average return of a portfolio component.
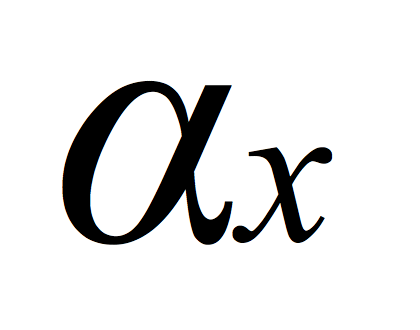is the portfolio component's drift.
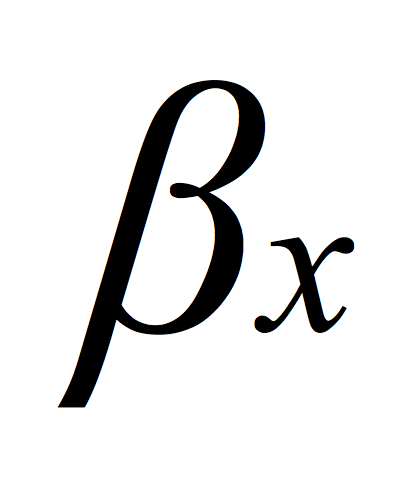is the portfolio component's linear systematic risk.
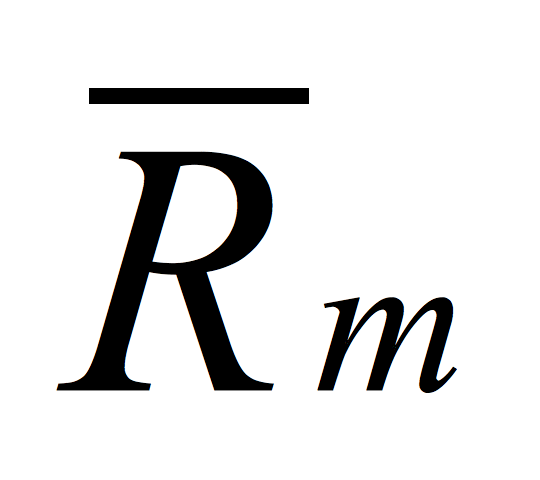is the average return of the market.
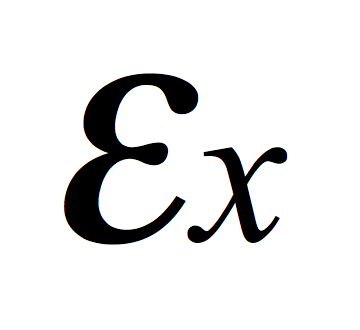is the portfolio component's error term.

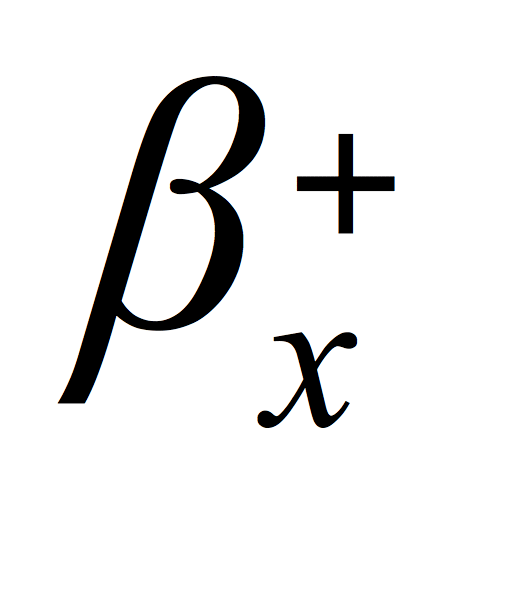then includes the assumptions of Elton/Gruber's market model (6th Ed p152: cov(e_i, e_j) <> 0) and develops the "Multifactor" equation below:

where:

is the portfolio component's positive linear systematic risk.
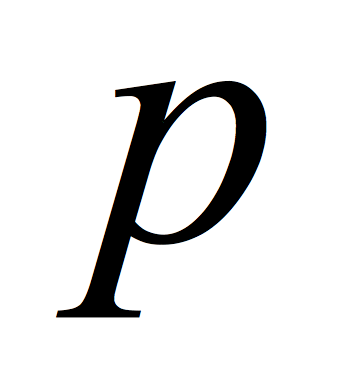is the probability of a rising market.
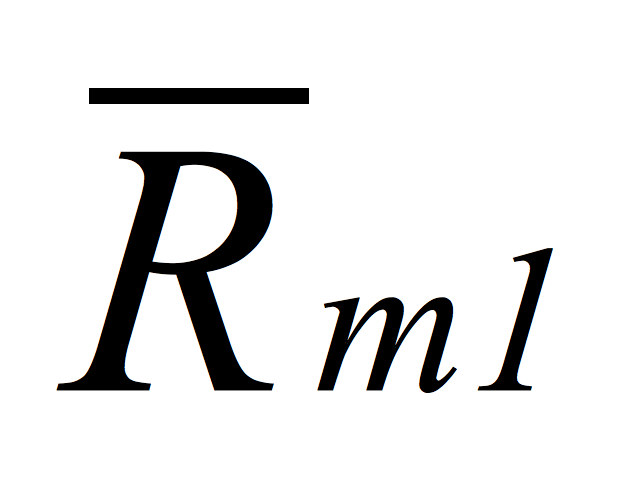is the average of the market's positive price changes.
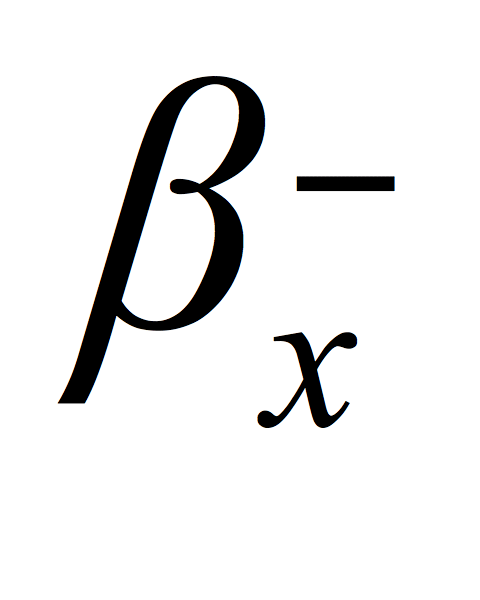is the portfolio component's negative linear systematic risk.
is the probability of a falling market.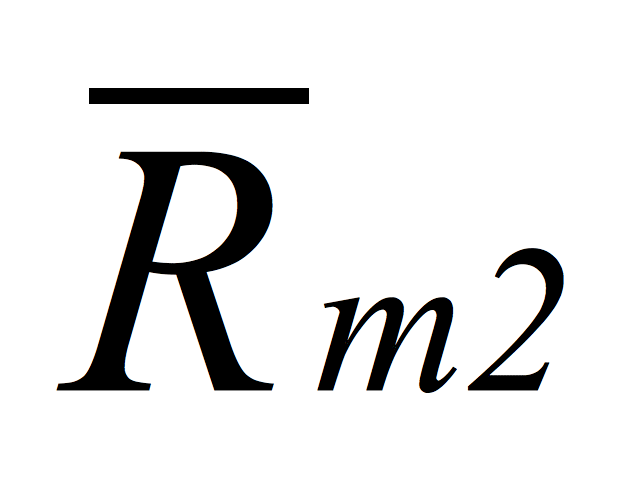
is the average of the market's negative price changes.

The Multifactor approach shows promise especially when compared to Rouwenhorst's Momentum Model and several models in Chapter 9 of Elton/Gruber. In particular, a Multifactor portfolio gained 9.75% while the Dow Jones Industrial Average lost 9.2% during the August-September 2015 correction.

Demonstration of the multifactor model during the August-September 2015 correction

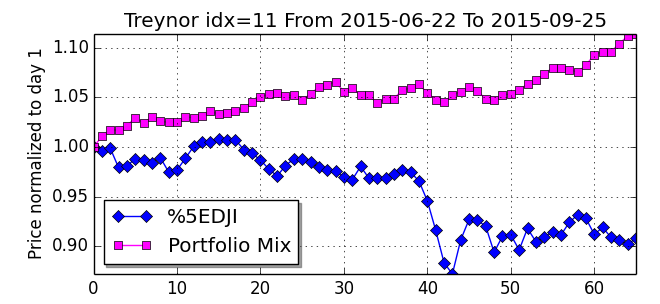
However, the standard questions plaguing all portfolio modeling approaches still remain:

What "training period" length should be used to calculate the above parameters?"
What is the portfolio component selection method?
What ranking method should be used to select the components with the appropriately high and low alphas?
How many components should go into a portfolio?
What is the best method to calculate p and q?
What is the holding period length? (test period)
How should one model corporate actions? (e.g. Corporate actions, dividend distributions, management, investments, merchantability, etc.)
How is the expected Rate of Return estimated?

These are questions that we would be interested in discussing and hearing feedback on. The model is discussed in more detail in English and German. Another useful paper (German) discusses how to maximize Return while ensuring solvency. Readers with sound input on these topics are welcome to submit their comments here.